Statistics Tutorials

Multi-omics studies are now common in large consortium studies as well as in smaller laboratories. As part of an online short course from the American Statistical Association (ASA) Section on Statistics in Genetics and Genomics (April 2023), we created materials to provide an introduction to commonly encountered multi-omics analysis topics, including a general multi-omics method overview, horizontal omics integration, multi-omics unsupervised clustering, multi-omics dimension reduction, multi-omics causal mediation and single cell multi-omics analysis. The first half of each lecture is a focus on the motivation, basic principles, representative tools, and applications. The second half of each lecture is lab session to provide hands-on experience.

All materials are available here: 

https://github.com/KechrisLab/ASAShortCourse-MultiOmics

To begin, we must first identify the differences between what statistics defines as population data and sample data. A population is the entire set people or things in a specified group. Characteristics of a population are called parameters. A sample is a subset of a population. Characteristics of a sample are called statistics.

Biostatistics is the use of statistics for public health, biological, or medical applications, and applied to a variety of research topics and fields. The main goal is to use appropriate statistical methods to understand the factors that affect human health.

Variable types

Qualitative (Categorical)

• Ordinal: Ordered categorical variables (ex. never, sometimes, frequently, always)
• Nominal: Unordered categorical variables (ex. hair color, gender)

Quantitative

• Continuous: Numerical variables with an infinite number of values (ex. height)
• Discrete: Numerical variables that can be counted (ex. number of bacteria)

Displaying data

• Tables: Numerical summary of frequencies, %, summary statistics, etc.
• Graphs: Visual representations of data:
• Histogram: Bar graph of frequencies
• Scatterplot: Plot of two numerical variables
• Boxplot: Visual representation of mean, median, quartiles, and range.

Study design

Observational study

• Observe an existing situation and makes inferences.
• Case Control: Study of existing groups differing on outcome (ex: patients with disease vs w/o)
• Cross-sectional: (prevalence) Study observing patients at a single point in time
• Cohort: Study that follows a group of similar individuals who differ with respect to certain factors, to determine how those factors affect an outcome of interest

Experimental study

Researcher randomly assigns individuals to treatment groups.

• Randomization: Technique used to select samples that keeps certain variables constant across groups (standardization) so true effect can be observed
• Placebo: Treatment given to a group that has no therapeutic effect
• Blinding: Treatment assignment is unknown to patient, doctor, or both

Hypothesis

Detailed prediction of a scientific question that can be tested.

• Null hypothesis: There is no relationship among the groups
• Alternative hypothesis: There is a relationship among groups
• P-value: Probability that the test shows a difference among the comparisons, assuming the null is true

Sample size justification

Method to ensure there are enough observations to find a statistical difference between groups when they are, in fact, biologically different.

Significance level (α): Threshold with which null hypothesis is rejected. Standard values for α include 0.05, 0.01, 0.001

• If the p-value is less than or equal to α, the null hypothesis is rejected
• If the p-value is greater than α, we fail to reject the null hypothesis

Power: Ability to detect a difference when a difference truly exists

Effect size: Clinically meaningful difference between comparisons

Study analysis

Bias

Any systematic error that can occur in multiple areas of a study, (e.g., study design, measurement technique, and or analyses) which will either over or under estimate a parameter and to false conclusions.

Descriptive statistics

Characterizing data using graphs, tables, numerical summaries.

Measure of Location
Mean: Average of the Data	Median: Middle point of the data	Mode: Most occurring data point
Measure of Spread
Standard deviation: Deviation of the data in a sample	Interquartile Range: Difference between the 75th percentile and the 25th percentile	Range: Difference between the largest and smallest values

Outliers: Very extreme data points

Frequency: The proportions of values within a single variable

Inferential statistics

Drawing conclusions about populations based on samples

• Confidence Intervals: Combining the sample statistics and standard errors to estimate population parameters
• Standard error: Uncertainty of the sample mean
• Statistical Tests: Tests used to quantify the similarity between comparisons
• Statistical test performed depends on variable type, number of comparisons, and underlying distribution of population
• Number of comparisons can be between two or more groups, independent or paired
• Distribution of population can be parametric (normally distributed), or non-parametric (no assumed distribution)
• Types of statistical tests: ttests, ztests, ftests, Chi-squared, ANOVA, Regression, Correlation, etc.

References
Baron, Anna. Biostatistical Methods. Lecture 1 Overview. Fall 2015.
Rosner. Fundamentals of Biostatistics. 7th ed. Brookes/Cole. 2011.
Samuels & Witmer. Statistics for the Life Sciences. 3rd ed. Pearson Education. 2003.

At the start of the study process, there are general questions, goals, and study aims that set the context for an idea. Often the questions seem clear but are not formulated in enough detail to perform analysis. Questions often range throughout research. Some examples are looking for results from groups with different profiles, assessing the effectiveness of a drug, or looking for a response pattern over time.

Supporting information is required to help move from the study aim to a hypothesis. A hypothesis is more detailed than a study aim. It is a testable, statistics-driven statement that will have evidence for or against, or no evidence at all.

Formulation of a hypothesis

Null hypothesis

• Accepted statistical practice for formulating a hypothesis is to start with a scenario of status-quo
• Often declares that the study will have no effect, e.g. no difference between groups, or no relationship between variables X and Y

Alternative hypothesis

• Is the compliment of the null hypothesis
• Often declares that the study will have an effect, e.g. there is a difference between groups, or there is a relationship between variables X and Y
• Characterizes how this effect will be manifested

Examples:

• Null: Drug X is no more effective for treating Disease W than Drug Y.
• Alternative: Drug X is more effective for treating Disease W than Drug Y.

It is critical to establish the null and alternative hypotheses before the study begins so that the appropriate measurements and controls can be put in place to ensure that the study is as unbiased as possible. Determining these hypotheses after the fact is a bit like ‘leading the witness’.

The primary goal of the study is to accept or reject the null hypothesis. It is through the rejection of the null hypothesis that there is enough evidence to support the possibility that the alternative hypothesis may be true.

Enrico Fermi had the following to say about hypothesis tests:
"There are two possible outcomes: if the result confirms the (null) hypothesis then you've made a measurement. If the result is contrary to the hypothesis, then you've made a discovery." 

Criteria for a hypothesis

A good hypothesis should have the following characteristics:

Characteristic	Examples
Be measurable: Define your independent and dependent variables, how you plan to measure them, and determine ways to examine the relationship between them.	Survival rates after treatment: 1,2,3 years Decrease in systolic blood pressure of a minimum of 5 mm Hg after 6 months
References a well-defined population: Describe in detail the members of the population   or contrast various population groupings.	Males age 55+ with family history of heart disease Pregnant women with elevated hormone levels Ethnicity - Existing conditions, comorbidity
Proposes cause-effect or association between variables: If not true cause and effect, then make a statement about the relationship or association between variables of interest, including potential predictor variables thought to have an impact on study outcomes.	Height Weight Genetic characteristics Vital measurements (potentially at different times during the study) History of smoking/tobacco use
Has a “biological” basis – or at least it’s plausible: Your hypothesis needs to be plausible and you need to have done your homework in the literature to propose it.	Examination of hereditary traits in an ethnic population Levels of serum beta-carotene distinguished in groups receiving 4 different treatments
Is clear, focused, and in the form of a statement: Refer back to the discussion of the null and alternative hypotheses to make a clear distinction between the two.	Treatment of Stage IV pancreatic cancer with drug X will result in a reduction of tumor size in treated mice compared to mice that were not treated.
Can answer at least part of your research question!: Sometimes a study might not have a specific hypothesis but will have an objective, perhaps just to provide descriptive statistics or to be exploratory. The study might just provide direction for follow-on work.	Describe the characteristics of Veterans Affairs patients who participated in open heart surgery for the last 6 months at hospitals in Colorado.

 

There are several different types of study designs which can be classified into two main categories: observational and experimental. Each study design has unique strengths and weaknesses which must be considered when determining the most appropriate design to test a study hypothesis.

Observational studies

Ecological

Studies of risk factors on health or other outcomes based on population or group (aggregate) data and not individual level data.

• Pro: Low cost, convenient, and hypothesis generating.
• Con: Heterogeneity of exposure and lack of covariates at the individual level.

Case series

Identify a group of individuals with an outcome of particular interest and describe the characteristics of the group. Studies with this type of design are based on prevalent cases since they represent a snapshot in time.

• Pro: Quick and easy, cheap to conduct, descriptive, and hypothesis generating.
• Con: Can’t assess causality, incidence-prevalence bias, and bias by time.

Cohort

Identify subjects before they have the outcome of interest, but they may be designed prospectively or based on retrospective data.

• Prospective: A sample is selected based on exposure status (exposed and unexposed/control group) and the study participants are followed "longitudinally" i.e., over a period of time, for disease development or outcome of interest.
• Retrospective: The investigators use data that has already been collected to identify a cohort of exposed/unexposed individuals at a point in time before they developed the outcome of interest (i.e., medical records) and then use the already collected follow-up data to calculate the risk of disease development.
• Pro: Temporality is established, multiple outcomes, can use when randomization is unethical, direct estimate of effect, rare exposures, and matching to control for confounding.
• Con: Time consuming and expensive (prospective), exposure not randomly assigned, confounding, selection bias, doesn’t work well for rare diseases, and loss to follow-up.

Case-control

Study that compares patients who have the disease of interest (cases) with patients who do not have the disease of interest (controls - who are from the same source population as the cases) and then looks back retrospectively to compare how frequently the exposure to a risk factor is present in each group to determine the relationship between the risk factor and disease. Studies with this type of design should use odds ratios to summarize the association between exposure and disease.

• Pro: Efficient, good for rare diseases, and can look at multiple exposures simultaneously.
• Con: Recall bias, differential misclassification of exposure status, hard to establish temporality, difficulty of selecting control group, and doesn’t work well for rare exposures.

Experimental studies

Randomized controlled trial

Study participants are randomly allocated to receive one or more treatment assignments that may include novel clinical interventions/treatments, placebo treatments, or existing interventions that serve as the standard of care. In randomized controlled trials, the investigator controls the exposure and then the study participants are followed-up for outcomes of interest. This type of study is generally considered the gold standard and is often used to test efficacy or effectiveness of various types of medical interventions.

• Pro: Gold standard, internally valid, temporality established, and minimization of confounding as participants are randomized to treatment groups.
• Con: Cannot use for unethical treatments, expensive, time consuming, often powered for efficacy and not adverse events, selection bias, and may lack external validity.
• Types:
  • Clinical trials (Drugs, FDA, etc. - subjects usually have disease or illness).
  • Field trials (Subjects not diseased, usually longer than clinical trials, involve visiting subjects in field i.e., home, work, etc.).

Crossover study/trial

A longitudinal study in which study participants receive a sequence of different treatments (or exposures) of interest during different time periods, i.e. the patients cross over from one treatment to another during the course of the trial with a predetermined "wash-out" period between treatments. This type of study design can be experimental or observational in nature.

• Pro: Cases serve as own control reducing confounding variables between subjects.
• Con: The "wash-out" period needs to be long enough to see independent effects of the two treatments and cannot be used for curative treatments since it would be unethical to randomize when the condition has been cured.

Quasi-experimental

Manipulate intervention but do not randomize subjects. Known as the "natural experiment" and exposure is often dictated by policy or legislation (e.g., seat belt laws).

• Pro: Less expensive than randomized trials, population-based, cost/benefit analysis, and fewer ethical issues than randomized trials.
• Con: Difficult to control for confounding.

Errors arising in various study designs

Random error: Natural variation in the underlying data the will be different for each sample.

Non-random error (systematic)

• Information bias (measurement error)
  • Subject/respondent bias
  • Recall bias
  • Reporting bias

Selection bias

Confounding: Distortion of the exposure-outcome association due to their mutual association with another factor. In order for a variable to be considered a confounder, it has to be associated with the exposure of interest and cause (or precede) the disease/outcome of interest.

Mediation: A mediator is present when the relationship between your exposure of interest (x) and your outcome (y) is mediated by a third variable (z). In other words, your mediation variable z is on the causal pathway between x and y.

 

Objective of tables

To clearly identify the measures and variables being used in a study and determine levels of confidence in reporting results.

To begin, let us look at an example of a Table 1. Typically, studies begin with a summary of the patient characteristics to show the properties of the sample being studied. This table is often referred to as "Table 1" and shows characteristics associated with the group of participants. Continuous and categorical variables are depicted in the table.

Suppose there is a drug treatment (Drug X) designed to reduce the risk of stroke among people aged 60 years or older with isolated systolic hypertension.

Table 1: Characteristics of Hypertension Participants

Baseline				After 6 Months
Characteristic	Active (N=2365)	Placebo (N=2371)	Total (N=4736)	Active (N=2330)	Placebo (N=23500	Total (N=4680)
Age, mean (SD), y	71.6 (6.7)	71.5 (6.7)	71.6 (6.7)	72 (6.7)	72 (6.7)	72 (6.7)
Systolic Blood Pressure, mean (SD), mmHg	170.5 (9.5)	170.1 (9.2)	170.3 (9.4)	160.5 (11)	170.1 (9.2)	165.3 (10.1)
Current Smokers (%)	12.6	12.9	12.7	12.5	12.2	12.3
Past Smokers (%)	36.6	37.6	37.1	36.2	36.3	36.2
Never Smokers (%)	50.8	49.6	50.2	51.3	51.5	51.5

General notes

• Label the table: Give each table a number and a title that concisely describes what the table represents.
• Footnote when necessary: Provide footnotes at the bottom of the table to provide explanations of table information.
• Refer to the table in the text: Refer to the table by number ("As Table 1 indicates…").
• Test Statistics: Report test statistics (t, F, x2, p) to 2 decimal places.
• Numerical precision should be consistent throughout the paper:
  Summary statistics (such as means) should not be given to more than one extra decimal place over the raw data.
• Standard deviations or standard errors may warrant more precise values.
• Regression analysis results also warrant precise values.
• Continuous variables: Summarize with means and report the standard deviation
• Categorical variables: Summarize with frequencies and percentages.

Simple graphs and correlation/association

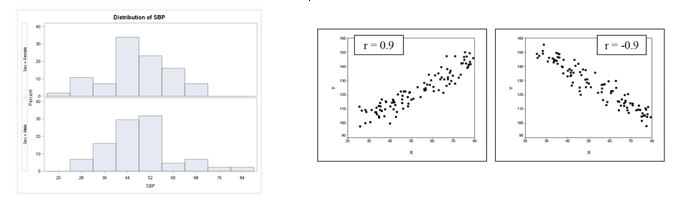
Study type

The use of simple graphs/visuals is a great way to get started with a set of data. For example, in the set of histograms above in which the Distribution of SBP is shown by gender, it spurs the question of why the two groups look a little different. By drawing out the linear relationship, one can start to see patterns of a positive or negative correlation between these two variables to start teasing out additional thoughts on why this would be true.

Confidence intervals

Confidence intervals are a range of values in which we feel confident that the true parameter is contained. It is important to distinguish confidence intervals from probabilities as we cannot attach a probability to the true value of the statistic based on a single sample of data. Confidence intervals are calculated in different ways depending on the type of statistic we are evaluating. In the example above, Systolic Blood Pressure (SBP) is a continuous variable for which a mean and standard deviation are given for the total participants in the study.

To calculate a confidence interval: Unknown mean (μ) and known standard deviation (σ)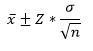


Note: x is the sample mean and the critical value (Z) for a 95% Confidence Interval is 1.96.

To calculate a confidence interval: Unknown mean (μ) and unknown standard deviation (σ)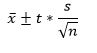
Note: When a proportion is the statistic being examined, confidence intervals are generated in a different way.

Benefit of confidence intervals

• The lack of precision of a sample statistic (for example: a mean) which results from the degree of variability in the factor being investigated and the limited study size, can be shown by a confidence interval.
  The width of a confidence interval is based on the standard error and the sample size.
• For more information, visit

Measures of difference and simple graphical presentation of results

Categorical vs. continuous data

• Categorical data is data that takes on a limited number of values. As the name would imply, the data fit into discrete categories. For example procedure type = "dental" and hospital = "Children’s Hospital" would categorical data. Categorical data can also be measured numerically. For example, ASA (an anesthesiology health score) can take on the values 1-5 and each patient is put into a category based on their health.
• Continuous data is data that can take on many values - too many to create specific categories. For example, pediatric doctors measure each patient’s height in centimeters, which can take on many different values up to 150 cm. So, height would be continuous data. Other examples include volume, cost, and time.
  Analyzing Categorical Data

Let’s go back to our ASA example which can take on the values 1-5. You want to look at the ASA values of patients at Children’s Hospital compared to those at University of Colorado Hospital. Your table would look something like this:

ASA	Children's Hospital	University of Colorado Hospital
1	20	36
2	34	49
3	23	19
4	15	14
5	0	2

This table describes how many patients fall into each category based on ASA value (the outcome) and hospital (the exposure). Now, you want to analyze your data—there are many ways to do this based on your research question.

Chi-square test

The chi-square test is used for categorical variables and tests whether ASA level is associated with hospital. In our example, we would be testing if ASA level differed between the two hospitals. It is important to pay attention to the cell counts, as the test expects at least 5 values in each cell. Since the cells coinciding with ASA values of 5 are 0 and 2, this test would not work. When the chi-square test is not an option, one may use Fisher’s exact test.

Risk ratio (RR)

Describes the risk of a certain event happening in one group compared to another.

• Risk 1=P(Disease | Exposed to causal factor)
• Risk 2=P(Disease | Not exposed to causal factor)
• Relative Risk Ratio = Risk1/Risk2

Interpretation

The risk of disease for a person exposed to the causal factor is (RR) times greater than for a person who was not exposed.

• Risk Difference = Risk1-Risk2 (interpreted as the excess risk in group one vs. group two)
• Odds Ratio (OR): The odds of having an event divided by the odds of not having that event.

Example:

• Odds Event 1: those who have cancer who got the treatment/those with cancer who did not get the treatment (A/B)
• Odds Event 2: those without cancer who got the treatment/those without cancer who did not get the treatment (C/D)
• OR = (A/B)/(C/D)

Interpretation: the odds of cancer are OR times lower in the group who got the treatment compared to the group that didn’t get the treatment.

Analyzing categorical data

T-test

• There are two types of common t-tests. If you are looking to see if you sample has a different mean than a population value, use a one sample t-test. 2) If you are looking to see if two populations have different means, use the two sample t-test. If your data is dependent (i.e. two measurements on the same person), use a paired two-sample t-test. Note: An ANOVA (analysis of variance) is an equivalent way to compare 3 or more groups

Regression techniques

• These are used when you are interested in the relationship between an outcome and its predictors (simple). Ex: does age predict ASA scores? Regression analyses are useful when you are interested in the effect of more than one predictor variable (multiple). Ex: do age and hospital predict ASA score?

Confidence intervals

Once you calculate an estimated mean or measure of association for categorical data, you can also calculate a confidence interval around that mean. This is important because it gives a measure of uncertainty about where the true mean lies. Once a confidence interval is calculated, it is read as "We have a certain level (i.e., 95%) of confidence that the true population parameter is within this interval."

Graphing data

• Scatterplot: used when graphing two continuous variables
• Bar Chart: visually compare groups
• Histogram: displays the distribution
• Box Plot: nicely displays mean, median, interquartile range, and outliers
• Line Graphs: primarily used for longitudinal data (tracking over time)

Know your assumptions. In general, we assume that the data were collected without bias, it is normally distributed for continuous variables and there are no unmeasured variables that actually explain the difference between the two means.

References
Roberts, Donna. "Qualitative vs Quantitative Data." Qualitative vs Quantitative Data. 2012. Web. 13 Oct. 2015.
"Risk Differences and Rate Differences." Risk Difference. Boston University School of Public Health, 16 Sept. 2015. Web. 13 Oct. 2015.
Szumilas, Magdalena. “Explaining Odds Ratios." Journal of the Canadian Academy of Child and Adolescent Psychiatry 19.3 (2010): 227–229. Print.
"Understanding Data Concepts." Understanding Data Concepts. Canada.ca, 9 Dec. 2013. Web. 13 Oct. 2015.

Aligning power or sample size analysis with planned data analysis helps to avoid the problems of 1) sample size too small to detect important alternative hypotheses and 2) sample size so large that the design squanders precious resources.

What do you need for sample size justification?

Discuss your science and study design before calculating your sample size. This information will be used to create  a table of sample size choices and a written paragraph justifying the sample size.

Data you need to provide from historical literature, pilot data, or other clinical information:

• Measures of variation (standard deviations) of the outcome measures.
• Estimate of a clinically meaningful difference between groups or an estimate of the size of association that is clinically meaningful (e.g., two-fold change).
• Estimates of correlation within individuals (or clusters) in studies with repeatedly collected measurements on an individual (or cluster). 

Sample size is a function of:

• Variation in outcome measures (and sometimes primary predictors)
• Size of a clinically meaningful difference between groups
• Level of significance (e.g., α = .05)
• Whether multiple tests are being performed (e.g., all genes in a gene expression study)
• Desired type II error (the probability that you will not find a difference when a difference in truth, exists) (e.g., β = 1 - power)

Important concepts
Based on the data, we make a decision to reject the null hypothesis (H0) or fail to reject H0. We quantify the evidence against the H0 in the form of a p-value. Remember, we want α and β small. Note: β increases as α decreases.

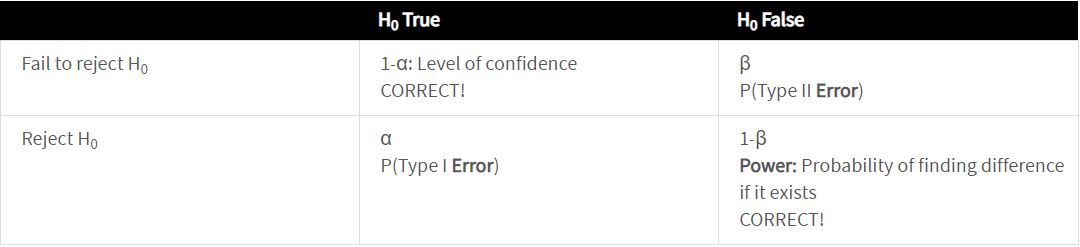
Evaluating the performance of a hypothesis test

There are 4 important quantities that vary together.

1. Level of significance of a test = α (usually 0.05)
2. Power of a test = 1 - β (usually 0.8 or 0.9)
3. Sample size = n
4. Detectable difference (sometimes called the effect size) = | μ0 - μ1 |
   • Based on prior knowledge
   • Based on preliminary study

Derivation of power for two-sided, one-sample Z-test

As an example, we illustrate derivations for a Z-test.  We usually set α (typically at 0.05), and then by fixing two of the other parameters we can calculate the last:

Power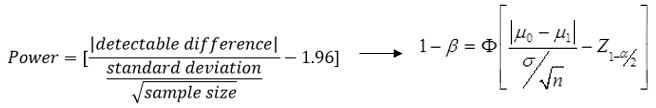

Detectable difference (difference in the means that can be detected)

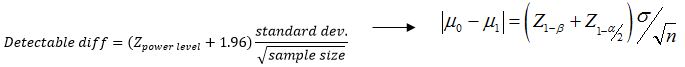
Sample size

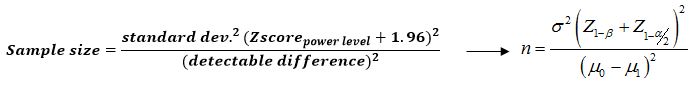Note: For a one sided test, replace α/2 with α.

How power, detectable difference, and sample size relate to each other:

As sample size n increases:

• Power: ⇧ Increases
• Detectable Difference | μ0 - μ1 |: ⇩ Decreases

As the difference to be detected | μ0 - μ1 |, increases:

• Power: ⇧ Increases
• Required Sample Size: ⇩ Decreases

As desired power increases:

• Required Sample Size: ⇧ Increases
• Detectable Difference | μ0 - μ1 |: ⇧ Increases

Common pitfalls

• Never ad-hoc the sample size even if you do not get a p-value you were hoping for. Remember, even if you do not show significance in your study you’re still providing the scientific community with useful and pertinent information while upholding the integrity of scientific inquiry.
• Having the minimum calculated sample size is not the most conservative approach. Having a larger sample size than the calculated value usually leads to a more robust and precise conclusion.
• The equations for calculating power, sample size, and detectable difference change depend on the proposed statistical test. Make sure to check assumptions for different tests prior to performing sample size or power calculations.

Useful references

• Sample size calculations: basic principles and common pitfalls. Nephrol Dial Transplant 2010. Topics addressed in this article: continuous vs. binary vs. other types of outcomes, different types of study designs, common pitfalls, reporting of sample size calculations
• PASS (Power Analysis and Sample Size Software)
• Free sample size and power calculator

What is reproducible research?

"Reproducible Research (RR) is the practice of distributing, along with a research publication, all data, software source code, and tools required to reproduce the results discussed in the publication. As such the RR package not only describes the research and its results, but becomes a complete laboratory in which the research can be reproduced and extended." (Source: CTSPedia)

Strive for your analysis to be reproducible and document your code.

Data management and data dictionary

Prepare your data for efficient analysis by creating a data dictionary prior to sharing your data. Data dictionaries give a list of variable names, type of variable (categorical, continuous, text), and interpretation of codes, e.g. 1="Female", 2="Male".

REDCap database development

Use REDCap to efficiently set up your database to make it easily accessible to your research team and usable for data analysis at the end of the study. REDCap is a secure web application for building and managing online surveys and databases.

If you want one of our biostatisticians to develop your database and forms for you, please submit our Request Biostatistics Consulting form and we will work with you to develop a scope of work and timeline for your project.

Possible analysis file structures

• “Wide” format: each row is an individual and any repeated measurements are presented in additional columns.
• “Long” format: each row is a single observation; thus individuals will have multiple rows if there are repeated observations on an individual (and some form of ID column signifies which observations belong to which subject).

Good data

• Datasets for analysis are best received as comma delimited text files (.csv extension).
• Columns cannot mix characters and numbers.
• Consistent capitalization is important; e.g. "Placebo" is different than “placebo” in data analysis.
• Choose variable names that reflect the measures for easier interpretation.
• Colors, bold, comments, etc. cannot be interpreted by statistical software.
• Each piece of information, such as group designation must be in a separate column.
• Missing data should be entered consistently for each variable. In comma delimited format a blank will be interpreted as a missing variable. Other common designations are ‘.’, "NA" or large negative numbers that are outside of the range of possible values, e.g. -999.
  

The Department of Biostatistics and Informatics offers an introductory applied statistics sequence designed for those without a calculus background and requires minimal mathematical derivations.

• Bios6601 - Applied Biostatistics I: descriptive statistics and enough basic analysis to create a Table 1 for a scientific paper.
• Bios6602 - Applied Biostatistics II: extends the basic principles of descriptive and inferential statistics to modeling more complex relationships using basic regression analyses.

More in-depth training is also taught in the MS biostatistics graduate courses. They require calculus and cover the theory of the methods in addition to the application.

Other applied courses are offered in longitudinal analysis, genetics/genomics analysis, etc.